
이번 포스팅에서는 수에 관련된 내용을 알아볼 것입니다.
수를 표현하는 집합인 수의 체계에 대한 내용을 주로 다루어 볼 것입니다.
주변에서 쉽게 볼 수 있는 정수, 음의 정수, 유리수, 0 등의 수에 대하여 자세히 알아보고, 이들을 이용한 연산에 대해서도 알아보겠습니다.
<목차>
1. 수의 체계
2. 연산의 성질
3. 합 연산
4. 곱 연산
5. 나누기 연산
1. 수의 체계
수의 체계는 그림으로 보았을 때 가장 간단하게 설명할 수 있습니다.

수의 체계에 대하여 이해하기 위해서 알아야 할 것이 있는데요. 바로 기수와 자릿수입니다.
먼저 기수는 숫자 체계에서 표현 근거를 알려주는 수를 말합니다. 숫자의 끝에 아래 첨자로 표기합니다.
다음으로 자릿수는 숫자의 각 자리가 갖는 값을 말합니다. 예를 들어 10진수 572를 기수와 자릿수로 표현하면
572 = 5 x 10²+ 7 x 10¹ + 2 x 10⁰ 이 됩니다. 이때 기수는 10이며, 자릿수는 10의 2 제곱, 1 제곱, 0 제곱의 2, 1, 0입니다.
1) 자연수( N )
자연수는 0보다 큰 양의 정수입니다.
n, b ∈ N, aᵢ ∈ N ∪ {0}이고, ㅠ>1, 0 ≤ aᵢ < b 일 때, n = aₖbᵏ + aₖ₋₁bᵏ⁻¹+ ... + a₁b¹ + a₀b⁰
(이때 aᵢ는 자연수 n을 구성하는 i번째 숫자이며 i는 0보다 크거나 같다.)
2) 정수( Z )
양의 정수, 0, 음의 정수로 구성된 수를 정수라고 합니다.
0에는 +,- 같은 부호가 붙지 않습니다. 그 이유는 0은 양의 정수나 음의 정수에 속하지 않는 수 이기 때문입니다.
-부호가 붙은 수는 0보다 작은 수는 음의 정수이고, +가 붙거나 부호가 생략된 양의 정수는 0보다 큰 수로 자연수와 같은 범위의 수입니다.
3) 유리수
a, b ∈ Z이고, a ≠ 0 일 때 b/a 인 수
즉, 정수의 원소인 임의의 값 a와 b가 있을 때, a, b를 이용하여 b/a로 나타낼 수 있는 수의 체계를 말합니다.
4) 무리수
a, b ∈ Z 이고, a ≠ 0 일 때 b/a로 표현할 수 없는 수를 말합니다.
ex) 4.7812392...,√2 등
5) 실수
유리수와 무리수를 모두 포함하는 수 체계를 말합니다. 소수점을 기준으로 왼쪽은 정수부, 오른쪽은 실수부입니다.
r ∈ R, aᵢ ∈ Z, b ∈ N이고, b > 1, 0 ≤ aᵢ ≤ b 일 때,
r = aₖbᵏ + aₖ₋₁bᵏ⁻¹ + ... + a₁b¹ + a₀b⁰ + a₋₁b⁻¹ + a₋₂b⁻² + ... (b는 기수이고, k는 자릿수입니다.)
이때, a₀b⁰부터 왼쪽은 정수부이며, a₋₁b⁻¹부터 오른쪽은 실수부입니다.
6) 허수
i² = -1을 만족하는 수 i를 허수라고 합니다.
제곱하여 음수가 되는 수는 없습니다. 그러나 물리학이나 전자공학 등의 학문에서는 제곱했을 때 0보다 작은 값이 되는 가상의 수가 필요한 경우가 있습니다. 이때 허수의 개념을 사용하여 방정식에 적용하여 사용하기도 합니다.
7) 복소수
실수와 허수를 모두 포함하는 수 체계를 복소수 라고 합니다.
c = a + bᵢ (c:복소수, a:실수부, bᵢ :허수부 / a, b ∈ R, c ∈ C)
b=0 이면 실수이고, b ≠ 0이면 허수입니다.
2. 연산의 성질
수를 연산한 결과는 수의 체계와 연산자의 종류에 따라 결정됩니다. 이때 알아야 할 성질이 연산의 닫힘 성질입니다.
수 체계 S에 속하는 어떤 수 a, b를 연산자 O로 연산한 결과가 S에 속하면 '수 체계 S는 연산자 O에 대해 닫혀있다.'라고 하고, 그렇지 않으면 '수 체계 S는 연산자 O에 대해 닫혀있지 않다.'라고 합니다.
이렇게 말로만 보면 잘 이해가 되지 않을 수 있습니다. 수의 체계별로 사칙연산의 닫힘 성질에 대하여 표로 정리해 보겠습니다.
| 덧셈 | 뺄셈 | 곱셈 | 나눗셈 | |
| 자연수 | O | X | O | X |
| 정수 | O | O | O | X |
| 유리수 | O | O | O | O |
| 무리수 | X | X | X | X |
| 실수 | O | O | O | O |
| 복소수 | O | O | O | O |
3. 합 연산
합연산 sigma는 Σ의 기호를 사용하며, 일정한 규칙이 있는 수열의 합을 말합니다.
시그마를 사용한 식은 아래와 같이 표현됩니다.

합 연산의 규칙이 있는데, 이에 대하여 알아보겠습니다.
c는 상수, x ᵢ ,y ᵢ ∈ R, k,n ∈ N 일 때,
1) c 상수가 n번 곱해집니다.
2) c 상수는 앞으로 시그마 앞으로 나올 수 있습니다.
3) 각각의 시그마 Σ에서 계산한 후에 계산할 수 있습니다.
4) 하나의 식을 두 개의 합연산을 더한 것으로 표현할 수 있습니다.
아래는 위의 4가지 규칙을 식으로 나타낸 것입니다.

4. 곱 연산
곱 연산은 프로덕트 Π 와 팩토리얼 ! 2가지로 할 수 있습니다.
먼저 프로덕트입니다. 기호로는 Π 를 사용하며, 곱 연산 프로덕트는 일정한 규칙이 있는 수열의 곱을 계산할 때 사용합니다. 아래와 같이 표기할 수 있습니다.
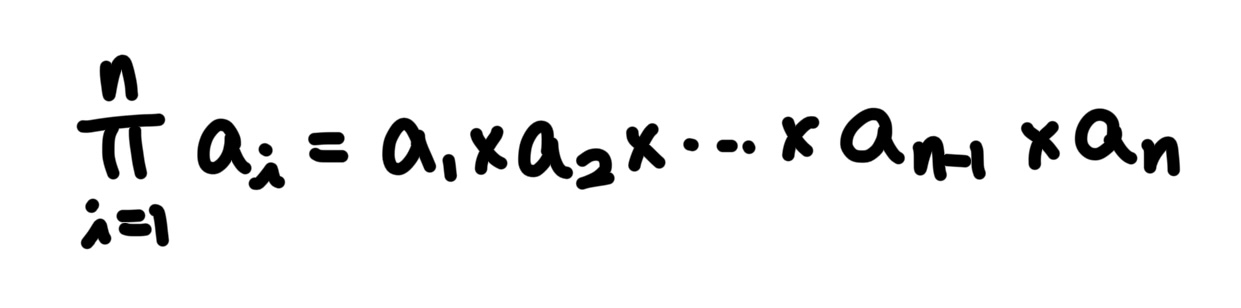
다음은 팩토리얼 입니다. 기호로는 ! 를 사용하며, n ∈ N 일 때, 1부터 n까지 1씩 증가하는 수열의 곱을 계산할 때 사용합니다.
n! = 1 x 2 x 3 x ... x n
5. 나누기 연산
나누기 연산은 몫을 구하는 연산과 나머지를 구하는 연산으로 볼 수 있습니다.
1) 몫을 구하는 연산
n = dq + r (n ∈ Z, d ∈ N, 0 ≤ r < |d|)을 만족하는 몫 q를 구하는 연산을 말하며, q = n div d입니다.
2) 나머지를 구하는 연산
n = dq + r (n ∈ Z, d ∈ N, 0 ≤ r < |d|)을 만족하는 나머지 r을 구하는 연산을 말하며, r = n mod d입니다.
'컴퓨터공학' 카테고리의 다른 글
| 멀티미디어, 정보의 표현 (0) | 2022.08.11 |
|---|---|
| 정보의 크기와 정보의 압축 (0) | 2022.08.05 |
| 진법간의 변환 방법 : 이진법, 10진법, 16진법 (0) | 2022.08.04 |
| 디지털 정보와 아날로그 정보 (0) | 2022.08.01 |
| 멀티미디어란 무엇일까? (0) | 2022.07.30 |










댓글